SwissBorg : Proof of Liabilities

À qui s'adresse ce rapport ?

Public cible : Tout le monde

Niveau technique : Moyen

Connaissances préalables : Des bases de cryptographie. Être à jour en matière d'informatique.

Ce document est destiné à être accessible à un éventail de lecteurs aussi large que possible. Ceci étant dit, il s'agit d'une explication très technique des processus de calcul qui nécessite que le lecteur ait un certain nombre de connaissances en information théorique et en cryptographie pour bien comprendre le sujet.

Introduction

Les récents événements dans le domaine de la crypto ont montré clairement que le public a le droit de savoir que leurs soldes sont sûrs, vérifiés et disponibles pour inspection. 

Dans le cadre de notre initiative de transparence appelée In SwissBorg We Trust, nous aimerions annoncer le lancement du portail Proof of Liabilities (preuve de passif) de SwissBorg, une solution de reporting web permettant à nos utilisateurs de voir leurs passifs, en s'assurant que leurs soldes ont été comptabilisés dans la somme totale.

Le protocole Proof of Liabilities montre essentiellement le total des passifs des utilisateurs et permet à tout utilisateur de valider que ses passifs sont comptabilisés dans le total, montrant ainsi qu’ils n'ont pas été omis du total ou diminués.

En accord avec la philosophie de SwissBorg, centrée sur la communauté, il est nécessaire que nos utilisateurs puissent vérifier eux-mêmes que leur passif est inclus dans notre PoL, sans avoir à compter sur un auditeur tiers pour le montrer. Rendre ce processus de vérification facile pour les utilisateurs a été un élément clé du mécanisme de validation de la PoL.

Dans la recherche de la meilleure solution, l'équipe d'ingénieurs de SwissBorg a créé un mécanisme de vérification de la PoL basé sur la technique cryptographique bien établie de l’“arbre de Merkle”, assurant ainsi une base technique solide et connue sur laquelle construire.

En ce qui concerne la mise en œuvre, nous avons choisi d'utiliser une solution web où le navigateur valide les passifs de l'utilisateur, offrant une transparence totale du processus de validation à quiconque souhaite voir et inspecter le code et les données.

Nous pensons qu'en utilisant ces méthodes robustes et fiables de validation et de mise en œuvre, notre solution PoL combine de la meilleure façon possible les approches de l'auto-vérification et de la facilité d'utilisation.

Ce post explique la conception cryptographique et les choix de conception de la solution PoL de SwissBorg, afin de vous permettre de mieux comprendre pourquoi et comment elle a vu le jour.

Si vous trouvez ce document trop technique, mais voulez quand même savoir comment valider, allez à la section "Comment valider" plus bas pour la marche à suivre.

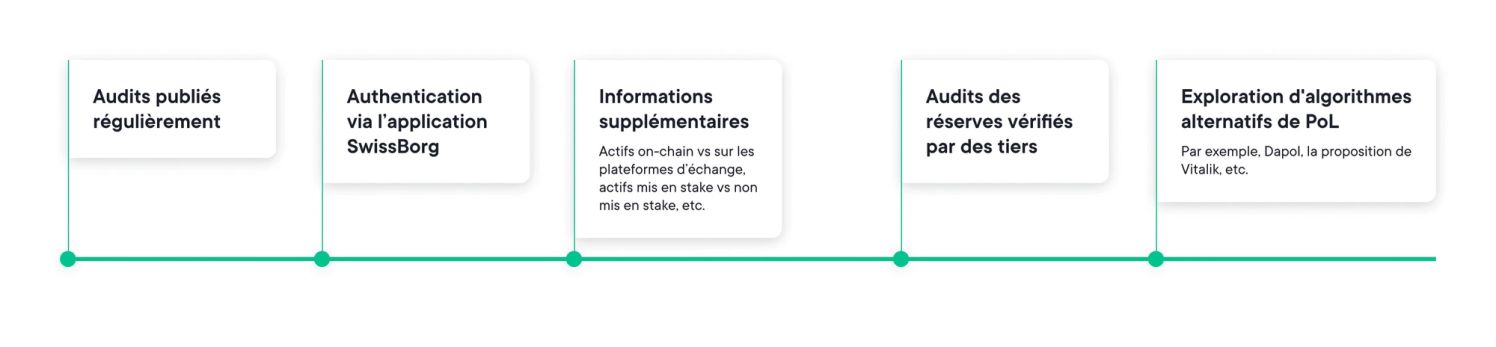
Voici une chronologie simplifiée pour vous donner un aperçu de nos plans pour l’avenir : 

Les bases

Un document ou un dashboard de preuve de passif (PoL) utilise un protocole qui interagit entre un Prover (prouveur) et des Verifiers (vérificateurs) pour montrer leurs passifs. Il va de soi que le prouveur fournit la preuve, et le vérificateur reçoit cette preuve et vérifie qu'elle est correcte. Dans notre cas, le prouveur est SwissBorg et les verifiers sont nos utilisateurs. 

Les passifs sont les soldes que les utilisateurs détiennent dans leurs portefeuilles et qui sont gérés par SwissBorg. La valeur de ces passifs, ou soldes, est simplement représentée par un nombre positif.

L'objectif principal du service PoL est de permettre aux utilisateurs de vérifier que leurs soldes sont pris en compte dans la somme totale des passifs de tous les utilisateurs. Essentiellement, une PoL fournit l'assurance que le prouveur ne peut pas avoir omis les passifs d'un utilisateur en vérifiant la PoL.

Déclaration du passif

La méthode la plus simple pour fournir un PoL est celle où la société montre publiquement combien chacun de ses utilisateurs détient, comme si votre banque montrait un relevé avec tous les avoirs de tous les clients. D'un point de vue plus technique, il s'agit d'une méthode où le prouveur montre une liste de tous les vérificateurs et de leurs passifs. Cette liste doit indiquer clairement toutes les informations, être accessible au public et, idéalement, être dynamique pour indiquer tous les changements.

Dans un exemple très simplifié, nous pouvons voir un grand livre de comptes, leurs valeurs associées et le total ; un grand livre où le prouveur a fourni les informations pour que tout le monde puisse les voir et les inspecter, et où les utilisateurs agissent en tant que vérificateurs pour s'assurer que les informations sont exactes.

Alice : 9 USD

Bob : 6 USD

Carlos : 7 USD

Diana : 4 USD

-----------------------

 Total : 26 USD

Dans cet exemple de base, il y a quelques points clés à considérer.

• Chaque utilisateur peut vérifier que son propre passif correspond à celui qui est indiqué et que la somme de tous les passifs correspond au montant total publié. 
• Si le prouveur omet ou fournit le passif d'un utilisateur inexacte, le prouveur est clairement responsable et risque de se faire prendre. 
• Cette approche élémentaire fonctionne, mais présente de sérieuses lacunes, notamment en matière de confidentialité.

Ci-dessous vous trouvez les attributs plus spécifiques de la PoL, qui sont cruciaux dans le processus de PoL pour les vérificateurs.

Vie privée

La divulgation d'informations financières avec les identités respectives des utilisateurs est clairement interdite et ne fait pas partie de notre processus de reportage de PoL.

Immuabilité

Un autre problème potentiel est la malléabilité des informations divulguées. En effet, le prouveur peut afficher différentes listes de passifs à différents utilisateurs dans le but de réduire la valeur réelle du total des passifs. Pour surmonter cette menace, nous devons introduire une "empreinte de données publiques" qui peut être vérifiée par chaque utilisateur afin de garantir que chacun a reçu le même ensemble de données. En informatique, le terme utilisé pour désigner ce type d'infrastructure de publication est un Public Bulletin Board (PBB).

Dans le cadre de ce sujet de l'immuabilité, il convient de mentionner deux propriétés supplémentaires qui doivent être mises en œuvre :

Soldes positifs

Une partie de la vérification de la somme des soldes des utilisateurs consiste à vérifier que chaque solde est positif. Il est possible pour un prouveur d'ajouter de fausses entrées - qui ne correspondent à aucun des utilisateurs - sans aucun risque d'être détecté.

Même si le prouveur pouvait ajouter ces fausses entrées, il n'aurait aucun intérêt à le faire car cela ne ferait qu'augmenter le passif qu'il détient. Du point de vue des utilisateurs, le prouveur semblerait moins solvable qu'il ne l'est en réalité, il n'y a donc pas de réelle incitation.

Unicité des identifiants des utilisateurs

Lorsqu'il y a une divulgation publique des passifs de tous les utilisateurs, tous les passifs individuels doivent bien sûr être liés à leur utilisateur spécifique par un identifiant. 

À ce sujet, le prouveur pourrait agir malicieusement. En supposant que deux utilisateurs différents aient exactement le même solde, ils pourraient tous deux se voir attribuer le même identifiant, devenant tous deux le même "utilisateur" avec la même preuve d'inclusion, ce qui permettrait à SwissBorg de diminuer effectivement la somme au sommet de l'arbre de Merkle et de ne comptabiliser les deux soldes d'utilisateurs qu'une seule fois.

Dans notre système, nous utilisons un identifiant d’utilisateur qui est unique et donc différent pour chaque utilisateur. Il s’agit de l’ID de l’utilisateur qui se trouve déjà dans l’application SwissBorg.

La Proof of Liabilities de SwissBorg

Conception de haut niveau

La conception spécifique du service Proof of Liabilities de SwissBorg est le résultat de l'utilisation de méthodes de pointe existantes, modifiées en fonction de nos exigences spécifiques - multi-devises, vérification dans le navigateur, pas d'auditeur externe - associées à la nécessité d'une mise en œuvre et d'un déploiement rapides. 

En analysant la littérature existante sur les protocoles PoL, il est apparu clairement que nous avions le choix entre deux options principales : 

• Le protocole standard basé sur un arbre de Merkle
• Basé sur une cryptographie avancée (par exemple, zk-snarks).

Le premier choix d'une approche standard basée sur un arbre de Merkle est dérivé de primitives cryptographiques établies qui peuvent être facilement mises en œuvre dans presque n'importe quel langage de programmation, tandis que les protocoles basés sur la cryptographie avancée nécessitent l'utilisation de bibliothèques cryptographiques "de niche" et avancées impliquant un effort de mise en œuvre beaucoup plus important.

Pour faciliter la décision, l'utilisation de primitives cryptographiques simples et bien comprises rend le résultat moins sujet à l'erreur. Pour cette raison, notre conception de PoL est basée sur la ligne de travail de l'arbre de Merkle initiée par la proposition Maxwell-Todd de 2013 telle que présentée par Gregory Maxwell et Peter Todd. Nous avons étudié la littérature existante et les implémentations de travail pour appliquer les dernières améliorations.

Qui est Merkle et pourquoi a-t-il un arbre ?

Les fonctions de hachage cryptographique sont l'ingrédient central de nombreux protocoles cryptographiques. Pour les non-initiés, une fonction de hachage est une fonction qui prend une entrée de taille quelconque et renvoie des données de sortie de taille fixe. Dans un exemple simplifié, une entrée de "Satoshi" produira les 4 chiffres 2341, et l'entrée de tout le texte du premier livre de Harry Potter ne produira également que les 4 chiffres 7654. 

Les valeurs hachées donnent des données de sortie de même longueur à partir d'entrées de longueur différente et la sortie ne peut pas être recouvrée jusqu'à l'entrée. Grâce à cette caractéristique, la sortie, également appelée hash (valeur hachée), est une empreinte unique de son entrée sur le plan informatique. 

Lorsque vous hachez des valeurs de hachage, une structure commence à se former, dont la taille diminue à chaque itération, ressemblant à des feuilles, des branches et un tronc. Au fur et à mesure de cette séquence, les données ne peuvent être modifiées à aucun moment du processus, sinon tous les hachages suivants changeraient également, ce qui conduit à une structure où les données d'entrée sont protégées contre toute modification.

L'introduction de l'arbre de Merkle remonte à l'invention de la cryptographie à clé publique à la fin des années 1970 et porte le nom de son inventeur Ralph Merkle. Dans sa forme la plus simple, un arbre de Merkle consiste en une structure de données de type arbre binaire où chaque feuille est le hachage d'un bloc de données et chaque nœud parent est le hachage des deux enfants :

Hparent = Hash ( HA | | HB ) [ if HA and HB are respective child hash values ]

Au sommet, l'élément racine (oui, nous savons que les racines de l'arbre se trouvent normalement au bas de l'arbre dans le sol) contient un hachage qui a essentiellement agrégé toutes les données sous-jacentes.

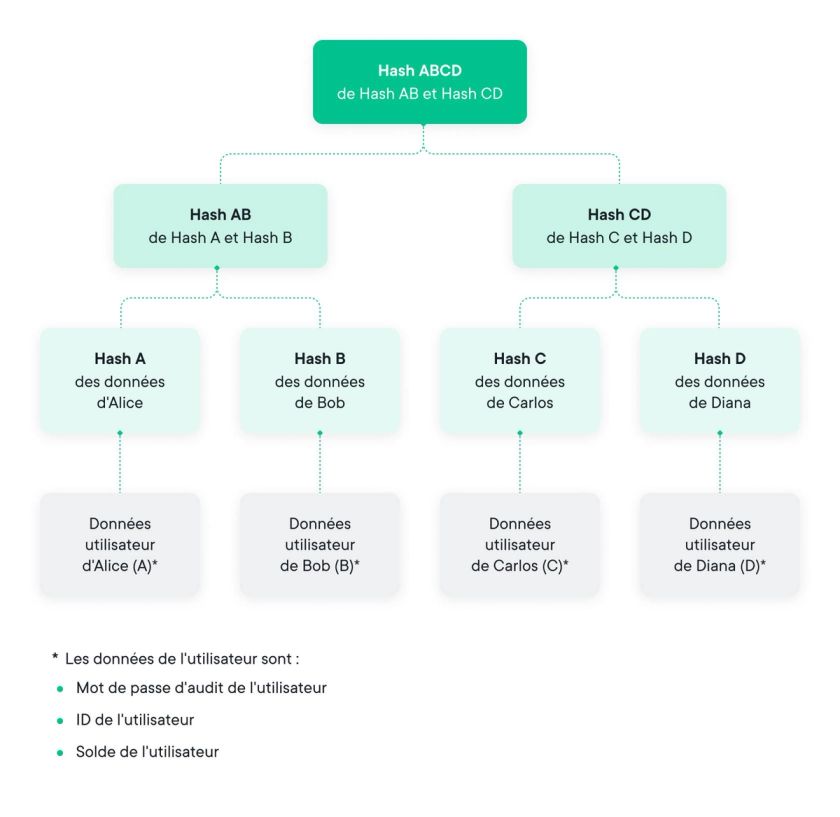
En raison des propriétés sous-jacentes des fonctions de hachage, il est impossible de modifier les données en un point quelconque de l'arbre sans modifier la valeur de hachage de la racine ; si quelque chose est modifié, le reste de la structure change. Jusqu'à présent, cela n'est pas très différent du hachage de toutes les données. Cependant, l'arbre de Merkle nous permet d'agréger un grand nombre de données - également appelées blocs - d'une manière très efficace pour vérifier l'inclusion d'un bloc de données spécifique. 

Autrement dit, cette méthode de vérification peut être utilisée pour démontrer qu'un bloc de données donné a été inclus dans l'arbre et que ce bloc se trouvait sur le chemin des nœuds frères successifs (sur le "chemin d'inclusion") jusqu'au valeur de hachage de la racine. De ce fait, la taille de la preuve d'inclusion devient logarithmique au lieu d'être linéaire ; ainsi, pour 1 million de feuilles, la preuve ne contient que 20 nœuds, sans compter le nœud racine.

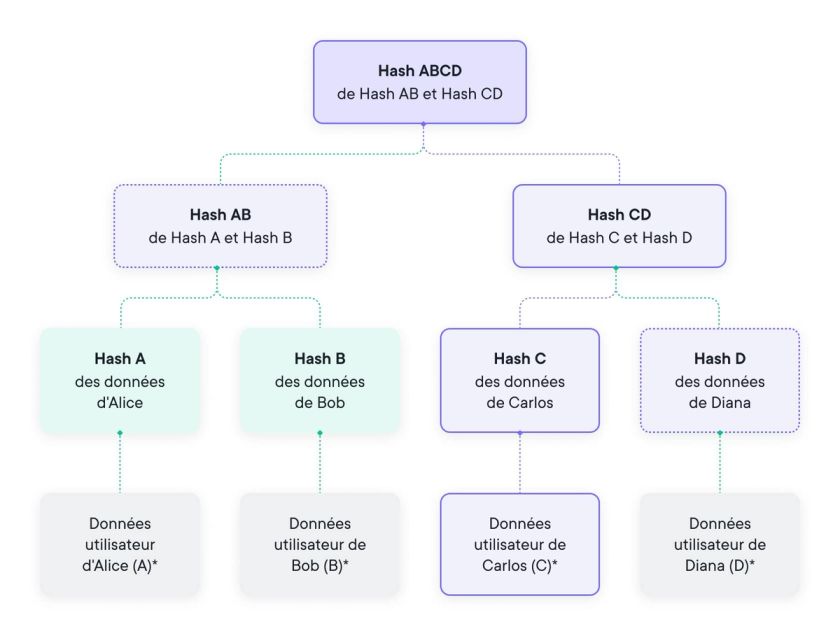
Au sommet de l'arbre, cette valeur de hachage de la racine agit comme un une mise en gage cryptographique car une fois cette valeur affichée, les données sous-jacentes ne peuvent plus être modifiées. D'autre part, il est impossible de prétendre que des données ont été incluses alors qu'elles ne l'étaient pas lors de la construction de l'arbre de Merkle, car elles sont toutes visibles et ne peuvent être modifiées.

La lignée Maxwell-Todd de la PoL

Comme mentionné ci-dessus, la première proposition de PoL basée sur un arbre de Merkle est attribuée à Maxwell-Todd en 2013. Leur proposition reposait sur l'utilisation d'un arbre de Merkle avec des blocs de données comprenant le solde d'un utilisateur. En outre, chaque nœud de cet arbre de Merkle est étendu avec un passif constitué de la somme de tous les passifs des nœuds enfants respectifs. Pour cette raison, chaque nœud est composé d'un digest (valeur de hachage) et d'un solde positif. 

De cette manière, le solde du nœud racine devient la somme de tous les passifs des utilisateurs. Cette structure de données est appelée "arbre de Merkle avec sommation", comme le montre le diagramme ci-dessous.

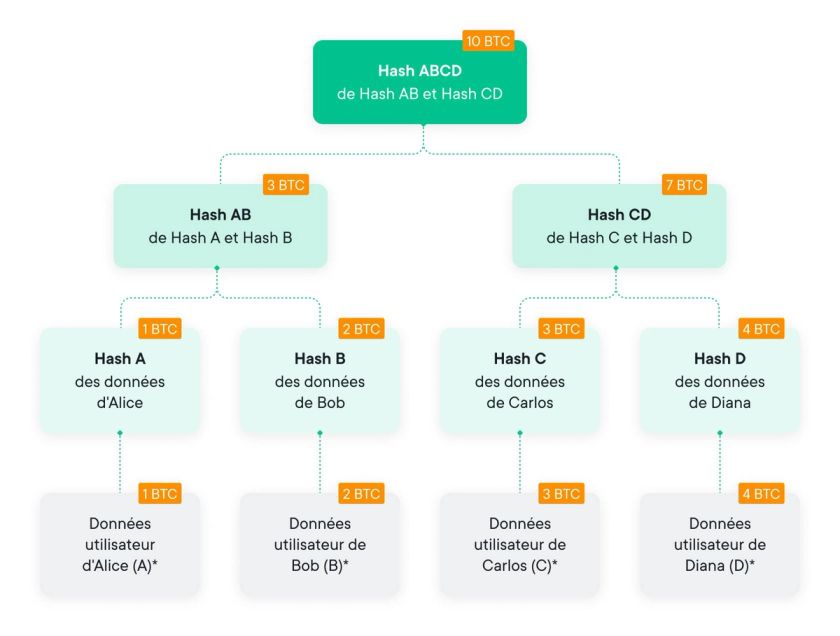
C'est là que les choses deviennent intéressantes. La valeur hachée d'un nœud feuille est obtenue en hachant l'identifiant de l'utilisateur, son mot de passe d’audit et son solde. Le mot de passe de l'utilisateur sert à masquer son ID, afin de protéger sa vie privée. Pour améliorer la sécurité de cette méthode, la position du nœud feuille d'un utilisateur donné est choisie au hasard pour rompre le lien entre un utilisateur et son solde. La valeur hachée de tout autre nœud est calculée en hachant les passifs des nœuds enfants et leurs valeurs digest respectives.

Hparent = Hash ( BalA | | BalB | | HA | | HB )

Pour montrer à un utilisateur que son passif est inclus dans l'arbre de Merkle, le prouveur fournit un chemin d'inclusion. Cela se fait de la même manière qu'avec un arbre de Merkle standard, mais avec la somme des dettes.

Dans la validation, l'utilisateur calcule le hash parent, comme ci-dessus, puis vérifie la sommation des soldes enfants. Dans le cadre de cette vérification de la somme, l'utilisateur vérifie également que BalA et BalB sont positifs et que BalA + BalB = Bal, où BalA, BalB sont les soldes enfants et Bal le passif du parent. Cette étape de validation est effectuée à chaque niveau de l'arbre de Merkle, des feuilles à la racine.

Nous notons que l'arbre de Merkle par sommation ci-dessus correspond à une version légèrement modifiée de l'arbre de Merkle Maxwell-Todd original en raison de l'application des idées présentées dans un article universitaire de Hu, Zhang et Guo (2019) qui a corrigé une faille de sécurité. La nouvelle variante de l'arbre de Merkle a été mise à jour avec la correction de cette faille de sécurité et a été baptisée "variante de Maxwell+" dans un article universitaire de Ji-Chalkias (2021) ; le nom est resté.

Poursuivant cette logique, l'article de Ji-Chalkias (2021) mentionne une méthode permettant de cacher les soldes originaux des utilisateurs en les divisant en plusieurs fragments - une idée attribuée à Chalkias, Lewi, Mohassel et Nikolaenko en 2019 - et en les mélangeant au hasard dans les feuilles de l'arbre. Suivant la logique de la nomenclature, cette variante suivante a été nommée la variante de Maxwell++ par Ji-Chalkias (2021).

Si l'on met tout cela bout à bout, on peut dire que la progression de cette méthode cryptographique en vue d'une utilisation pratique sur les Proof of Liabilities est apparue avec l'itération de Maxwell-Todd, où l'arbre de Merkle a pu inclure la sommation. En poursuivant la chronologie de l'innovation, une faille de sécurité a été découverte et corrigée, ce qui a conduit à l'établissement et à l'utilisation de la variante Maxwell+, et la version finale dans laquelle le solde de chaque utilisateur est divisé en fragments afin de masquer le passif réel de l'utilisateur a donné naissance à Maxwell++. Chacune de ces améliorations a été importante et bien accueillie par la communauté. Nous sommes heureux d'utiliser cette technologie dans notre solution également.

Les choix de conception de SwissBorg

Comme la plateforme SwissBorg supporte plus de 70 devises fiat et cryptoactifs, les utilisateurs possèdent généralement un certain nombre d'entre elles. En principe, nous pourrions appliquer un seul arbre de Merkle pour couvrir toutes les devises en même temps en appliquant la somme des soldes, par devise. Cependant, pour de nombreux utilisateurs, la répartition des devises dans leur portefeuille est unique et poserait donc un sérieux problème de confidentialité.

Notre conception traite chaque devise séparément en construisant un arbre de Merkle dédié par devise. Nous agrégeons ensuite toutes les racines des différents arbres de Merkle dans un Audit Commitment Hash, qui est la valeur de hachage des totaux des passifs par devise et des valeurs de hachage respectives des racines des différents arbres.

Essentiellement, l'ensemble de la construction peut être considéré comme un seul arbre de Merkle, à la différence que la couche supérieure est constituée d'autant de branches que le nombre de devises. En raison de cette caractéristique, afin de vérifier les passifs, toutes les racines des arbres de Merkle des devises doivent être envoyées dans le cadre de la preuve d'inclusion.

Pour améliorer encore la confidentialité des soldes des utilisateurs, nous divisons chaque solde d'utilisateur en au moins 2 sous-soldes/shards positifs et leurs positions dans les feuilles de l'arbre de Merkle sont déterminées au hasard. Par souci de simplicité et pour cacher partiellement le nombre d'utilisateurs par devise, nous générons toujours un nombre de sous-soldes égal à une puissance de 2 afin que l'arbre binaire de Merkle soit complet.

Il est intéressant de noter que la division des soldes est conforme à la solution PoL de Bitmex et à la variante Maxwell++ avec un facteur de division > 2.

Selon la conception de Maxwell++, la confidentialité de l'utilisateur est assurée par l'inclusion de nonces de masquage à haute entropie dans les données feuilles ; sur la base d'un nœud feuille - le hash et le solde - il n'est pas possible de découvrir l'identité de l'utilisateur correspondant. Ce "nonce de feuille" est dérivé d'un identifiant d'audit par utilisateur, une sorte de mot de passe qui est une valeur aléatoire de 128 bits exclusivement réservée aux besoins de la PoL.

Où puis-je trouver mon mot de passe d’audit ?

Votre mot de passe se trouve dans l'onglet Sécurité de l'application SwissBorg. Vous devez le garder confidentiel car quelqu'un pourrait le prendre et l'utiliser pour révéler vos soldes - avec les nœuds feuilles correspondants.

Ce mot de passe est destiné à être conservé à long terme et réutilisé dans le cadre de plusieurs audits de PoL. Conformément aux pratiques cryptographiques standard, les nonces des feuilles sont dérivés - avec une fonction de dérivation de clé cryptographique (Key Derivation Function) - de manière hiérarchique :

• Identifiant d'audit, mot de passe d'audit de l'utilisateur → Nonce d'audit.
• Nonce d’audit, devise → Nonce de l’arbre de Merkle
• Nonce de l’arbre de Merkle, indice de feuille → Nonce de nœud feuille
• Données feuilles : nonce feuille, userID, sous-solde

Un autre détail important est que ces différents niveaux de nonces peuvent être utilisés pour révéler des informations liées au passif de l'utilisateur à différentes spécificités, par exemple par audit ou par devise.

Bien sûr, tout le monde a besoin d'un identifiant d'utilisateur, et pour cela nous avons choisi d'utiliser l'ID de l'utilisateur SwissBorg, qui est associé à tous les stades du processus et peut être facilement trouvé dans l'application sur l'onglet Profil en bas de l’écran sous la forme ID : 20XXX. Cet identifiant ne change jamais et est unique pour chaque utilisateur.

Le service PoL de SwissBorg fournit plusieurs chemins d'inclusion de l'arbre de Merkle, un par shard de sous-solde de l'utilisateur en fait, qui sera validé par un script exécuté dans le navigateur et rendra les soldes totaux pour cet utilisateur.

Le contrôle de validation est effectué par rapport aux Audit Commitment Hashes qui seront rendus publics via Twitter. L'algorithme peut être résumé comme suit :

1. Tous les nœuds racines de Merkle sont vérifiés par rapport à l’ "Audit Commitment Hash". En outre, l'utilisateur peut vérifier que ce hash correspond à celui publié sur Twitter.
2. Pour chaque chemin d'inclusion, le chemin est validé en calculant récursivement le nœud parent avec le nœud frère fourni par la preuve d'inclusion et en vérifiant que le nœud supérieur correspond à l'un des nœuds racines de l'arbre de Merkle qui ont été validés à l'étape précédente. Dans le cadre de ce processus, une vérification est effectuée pour chaque frère afin de s'assurer qu'ils ont un passif positif.
3. Après chaque validation réussie de la preuve d'inclusion, le solde feuille de l'utilisateur correspondant est ajouté au passif total de l'utilisateur.
4. Si aucune erreur ne s'est produite, le total du passif de l'utilisateur lui est rendu.

Discussion

La conception de la Proof of Liabilities de SwissBorg est basée sur l'état de l'art de la construction d’arbre de Merkle, assurant la plus grande confidentialité des identités des utilisateurs et des passifs associés. De plus, nous avons choisi de mettre l'accent sur la facilité d'utilisation et l'auto-vérification par l'utilisateur, ce qui signifie qu'aucun auditeur tiers ne doit être impliqué, contrairement à plusieurs autres solutions de PoL comme celle de Kraken par exemple.

Notre approche est plus conforme à celle de Bitmex, la principale différence étant que notre vérification est plus légère et s'adapte à un environnement multi-devises.

Cette caractéristique de légèreté vient du fait que l'utilisateur n'a pas à télécharger un arbre de Merkle complet, mais seulement des preuves d'inclusion qui représentent une petite fraction de l'arbre. Cela permet une validation dans le navigateur qui peut être inspectée par l'utilisateur s'il le souhaite.

Nous sommes arrivés à la conclusion que le fait de ne pas publier les arbres de Merkle complets ne constitue en aucun cas une vulnérabilité, car l’ "Audit Commitment Hash" garantit l'intégrité des données sous-jacentes - il est cryptographiquement impossible de modifier ultérieurement les données de l'arbre de Merkle. 

La divulgation de l'arbre de Merkle complet ne peut que garantir que la structure est bien formée, en ce sens que tous les passifs sont positifs et que les hachages des nœuds non-feuilles sont corrects.

Limitations

En termes de limitations, un utilisateur qui effectue la validation ne peut pas détecter si le passif d'un autre utilisateur est inexacte ou a été omis. Pour détecter un cas de manipulation par un fournisseur malveillant, il faut une validation par les utilisateurs concernés, indépendamment de la publication de l'arbre de Merkle complet ou de la divulgation des preuves d'inclusion.

L'assurance que le nombre total de passifs ou la valeur totale des passifs n'ont pas été diminuées par le fournisseur dépend du niveau d'implication des utilisateurs. 

Avec ce système d'auto-vérification sans tiers, uniquement à preuve d'inclusion, plus le nombre d'utilisateurs qui vérifient leurs passifs est élevé, mieux c'est. En effet, plus il y a de personnes qui regardent les informations, plus il y a de chances que si quelque chose ne va pas, cela soit vu, d'où un plus grand consensus des utilisateurs.

Cela revient au concept de base suivant : "plus il y a de personnes qui vérifient quelque chose, moins il y a de chances que le prouveur puisse le modifier sans être remarqué".

Dans la section 5 de l'article universitaire de Ji-Chalkias mentionné précédemment, les auteurs présentent des calculs détaillés sur le nombre d'utilisateurs effectuant des vérifications de preuves d'inclusion nécessaires pour détecter toute mauvaise conduite de la part du prouveur.

Notre solution présente des limitations supplémentaires qui ne menacent pas la sécurité et qui font l'objet d'une recherche constante d'améliorations. Ces limitations concernent :

• certaines informations sur les passifs individuels - sans aucun lien avec les identifiants des utilisateurs,
• la confidentialité du nombre d'utilisateurs par devise,
• le total des passifs.

Selon nous, le premier point de la liste, à savoir la limitation de la confidentialité des informations sur les passifs individuels, a été résolu grâce à notre solution de "fractionnement des soldes", qui affiche toujours des informations partielles, comme l'indication d'un solde supérieur à un certain montant, mais pas de données personnelles sensibles.

Pour clarifier, le fractionnement des soldes signifie simplement que le solde original de l'utilisateur est fragmenté en sous-soldes de sorte que la somme des sous-soldes = le solde original. Ainsi, le solde d'origine n'apparaît pas dans l'arbre de Merkle. 

Les deuxième et troisième limitations concernent davantage les informations que le fournisseur pourrait vouloir garder privées et ne posent pas de réel risque pour la vie privée de nos utilisateurs. La bonne nouvelle est qu'il existe des solutions modernes basées sur des constructions cryptographiques plus avancées, comme zk-SNARKS, qui résolvent ces problèmes, ce qui nous donne la possibilité, à l’avenir, de mettre en œuvre et de réduire encore ces limitations.

Pour l'instant, en raison de leur nouveauté, ces solutions sont moins accessibles et nécessitent davantage de développement de notre part. Pour ces raisons, nous avons décidé de mettre en œuvre d'abord la solution éprouvée de l'arbre de Merkle, car les problèmes restants ne sont pas du tout critiques.

Nous gardons un œil sur toutes ces solutions, y compris la proposition très discutée de Vitalik et la très prometteuse solution Dapol+ de Ji-Chalkias, qui a attiré l'attention de la communauté crypto lors de la Computer and Communications Security Conference, ACM CCS 2021. Nous continuerons à innover notre solution, en intégrant les améliorations au fur et à mesure qu'elles arrivent ; nous avançons toujours vers le futur.

Pourquoi pas d'auditeurs tiers ? 

Si l'auto-vérification par les utilisateurs était une exigence stricte de notre système, cela n'exclut pas la possibilité de l'implication d'un auditeur tiers à l'avenir. L'un des avantages potentiels de l'arrivée d'un tel organisme est d'accroître les pouvoirs de détection et de ne pas compter uniquement sur la participation des utilisateurs pour détecter un fournisseur frauduleux. 

Voici quelques bons exemples de cette influence positive.

• Un auditeur tiers pourrait vérifier systématiquement un échantillon des passifs des utilisateurs par rapport à la PoL.
• L'implication d'un auditeur en cas de résolution d'un litige par lequel un utilisateur déclare des passifs inexactes ou manquants dans le rapport de PoL.

Il semble qu'un problème de ce type soit difficile à résoudre par des moyens purement techniques et que l'intervention d'un auditeur tiers soit d'une grande utilité. Pour approfondir ce point, dans l'analyse de sécurité de Chalkias de la PoL de Binance, il évoque le fait que l'implication d'un auditeur pourrait empêcher le fournisseur de suivre les utilisateurs qui effectuent la vérification, et omettre les passifs de ceux qui ne vérifient jamais. Autant de choses à considérer pour les futures itérations.

Comment valider

En tant qu'utilisateur, vous pouvez vérifier et valider vos passifs en visitant la page “En sécurité avec SwissBorg” sur notre site web. 

Veuillez suivre les instructions de la page et saisir votre mot de passe d'audit personnalisé, que vous trouverez dans la section Sécurité de l'application SwissBorg.

Il est important de savoir que les passifs que vous verrez sont pris au moment du dernier audit et ne sont donc pas une représentation en temps réel de vos passifs. Ces audits sont prévus de façon régulière, la fréquence sera annoncée lorsqu'elle sera définitivement déterminée.

Si vous connaissez le terme "GitHub repo" et que vous souhaitez vérifier et valider vos passifs localement sur votre ordinateur, veuillez suivre les instructions du code source publié SwissBorg Proof of Liabilities Repo.

Remarques finales

Prouver ce que nous détenons pour nos utilisateurs est devenu une pratique standard dans l'espace crypto, et nous sommes fiers d'avoir construit indépendamment une solution qui offre aux utilisateurs la possibilité de vérifier leurs avoirs.

La première version du portail Proof of Liabilities de SwissBorg a été publiée, permettant à chaque utilisateur de valider facilement ses passifs correspondants sans dépendre de vérificateurs tiers, tout en atteignant un niveau élevé de sécurité et de confidentialité.

Il s'agit d'une initiative en évolution et nous surveillons ses développements potentiels. En particulier, nous pourrions envisager de mettre en œuvre, à l’avenir, l'une des techniques cryptographiques les plus avancées pour renforcer le système, comme la proposition de Vitalik. 

Avoir des preuves sécurisées, ouvertes, simples et centrées sur l'utilisateur est un sujet crucial, sur lequel travaillent de nombreux acteurs et sous plusieurs angles. Cela dit, il faudra peut-être un certain temps avant que le secteur ne converge vers la standardisation des PoL, mais nous considérons qu'il s'agit d'une évolution positive inévitable, pour tout le monde.

Pour l'instant, tout le monde compte sur tout le monde, ce qui signifie que nous comptons sur nos formidables utilisateurs pour prendre un moment et valider leurs passifs à travers le portail Proof of Liabilities, et ce faisant, savoir qu'ils ne font pas que s'assurer que leurs cryptoactifs sont en sécurité et comptabilisés, mais qu'ils contribuent également au renforcement de la confiance en SwissBorg et notre incroyable communauté.

Disclaimer

Veuillez noter que les informations relatives aux passifs des utilisateurs fournies par notre protocole de Proof of Liabilities sont enregistrées à partir du ledger interne de SwissBorg. SwissBorg ne peut être tenu pour responsable d’éventuels soldes erronés qui résulteraient d'une erreur ou d'une faute dans le ledger. Le protocole de Proof of Liabilities ne fournit pas d'informations sur les autres passifs de l’entreprise ou les autres risques auxquels l'entreprise est confrontée. Les informations contenues dans ou fournies à partir de ou via cet article (l'"Article") sont fournies à titre informatif uniquement et ne constituent pas des conseils financiers, des conseils en investissement ou tout autre type de conseil et ne doivent pas être interprétées ou comprises comme une quelconque forme de promotion, recommandation, incitation, offre ou invitation à (i) acheter ou vendre un produit, (ii) effectuer des transactions, ou (iii) s'engager dans toute autre transaction légale. Ni SwissBorg Solutions OÜ ni ses entités affiliées ne font de déclaration ou ne donnent de garantie quant à l'exhaustivité, l'exactitude, l'actualité ou l'adéquation de toute information contenue dans une partie quelconque de l'Article, ni à l'absence d'erreur.