Who is this report for?
Reader: Everyone.
Technical Level: Medium.
Prior Knowledge: Some cryptography.
Being up to date on computer science.
This document is meant to be accessible to as wide a range of readers as possible. That being said, this is a technical explanation of computational processes requiring the reader to have a certain amount of knowledge of computer theory and cryptography to fully understand the subject matter.
Check how our Proof of Liabilities portal works
Introduction
Recent events in crypto have made it perfectly clear that the public has a right to know their balances are safe, checked and available for inspection.
As part of our transparency initiative called In SwissBorg We Trust, we’d like to announce the launch of the SwissBorg Proof of Liabilities Portal, a web reporting solution enabling our users to see their liabilities, ensuring their balances have been accounted for in the total sum.
A Proof of Liabilities protocol essentially shows the total user liabilities and lets any user validate that their liabilities are accounted for in the total, in effect showing that their liabilities were not omitted from the total or lowered.
In line with SwissBorg’s community-centric philosophy, it has long been a requirement that our users can self-verify that their liabilities are included in our PoL, without having to rely on a third-party auditor to show them. Making this checking process easy for users has been a key part of the PoL validation mechanism.
In the search for the right solution, the SwissBorg engineering team has created a PoL verification mechanism based on well-established Merkle Tree cryptographic techniques, ensuring a solid and known technical foundation on which to build.
On the topic of implementation, we chose to use a web-based solution where the browser validates user liabilities, giving full transparency of the validation process to anyone who wants to see and inspect the code and data.
We believe by using these sturdy and reliable methods of validation and implementation, our PoL solution combines approaches to self-verification and smooth usability in the best possible way.
This post explains the cryptographic design and build choices made for the SwissBorg Proof of Liabilities solution, in an effort to give you a better understanding of why and how it came to be.
If you find this document too technical, but still want to know how to validate, go to section “How to validate” further down for the steps.
Putting things into a timeframe, our next steps are outlined on the timeline below:
The Basics
A Proof of Liabilities (PoL) document or dashboard uses a protocol that interacts between a Prover and the Verifiers to show the liabilities between the two. It stands to reason that the Prover provides the proof, and the Verifier receives this proof and checks that it is correct. In our case, the Prover is SwissBorg and the Verifiers are our users.
Liabilities are the balances that users hold in their wallets that are managed by SwissBorg. The value of these liabilities, or balances, is simply represented by a positive number.
The main goal of the PoL service is to allow users to verify that their balances are accounted for in the total sum of all users’ liabilities. Essentially, a PoL provides assurance that the Prover could not have omitted a user’s liabilities.
Disclosure of Liabilities
The simplest method for providing a PoL is one where the company publicly shows how much each of its users holds, like if your bank showed a statement with all the holdings of all the clients. Put in a more technical way, it’s one where the Prover shows a list of all the Verifiers and their liabilities. This list must clearly show all the information, be openly available to the public, and ideally be kept dynamic to show any and all changes.
In a very simplified example, we can see a ledger of accounts, their associated values, and the total; a ledger where the Prover has provided the information for all to see and inspect, and where the users act as Verifiers to make sure the information is accurate.
Alice: 9 USD
Bob: 6 USD
Carlos: 7 USD
Diana: 4 USD
----------------------
Total: 26 USD
Within this basic example there are some key points to consider.
- Each user can verify that their own liabilities match those listed and that all liabilities add up to the total published amount.
- If the Prover omits or provides the incorrect users' liabilities, the Prover is clearly responsible and takes the risk of being caught.
- This elemental approach does the job, but presents serious shortcomings, in particular in regard to privacy.
Looking at the more specific attributes of PoL, the topics below show the crucial qualities that must be used in the PoL process and disclosed to the Verifiers.
Privacy
The disclosure of financial information with respective user identities is clearly a no-go, and not part of our PoL reporting process.
Immutability
Another potential issue is the malleability of the disclosed information. In effect, the Prover may display different lists of liabilities to different users in an attempt to reduce the real value of the total of liabilities. To overcome this threat, we need to introduce a ‘public data fingerprint' which can be verified by each and every user to guarantee that everyone has received the same data set. In computer science, the term used to designate this type of publication infrastructure is a Public Bulletin Board (PBB).
Within this topic of immutability, it is worth mentioning two additional properties that need to be enforced:
Positive Balances
Part of the verification of the sum of users’ balances is a check that every balance is positive. It is possible for a malicious Prover to add fake entries – which correspond to none of the users – without any risk of being detected.
Even though the Prover could add these fake entries, there would be no incentive for the Prover to do so as this would only increase the liabilities they hold. From the users' perspective, the only thing that would change is that the Prover would seem less solvent than they actually were, so there is no real incentive.
Uniqueness of Users Identifiers
When there is a public disclosure of all users’ liabilities, all the individual liabilities of course need to be linked to their specific user through an identifier.
Within this topic, there is a mischievous move the Prover could make. Assuming two different users had the exact same balance, they could both be assigned the same identifier and therefore becoming the same ‘user’ with the same inclusion proof, allowing SwissBorg to effectively decrease the sum at the top of the Merkle Tree. We would account both user balances only once.
With our system the user identifier is both unique to an individual users and to our system, making it singular and separable from other users.
SwissBorg’s Proof of Liabilities
High-level design choices
The specific design of the SwissBorg Proof of Liabilities service is the result of using existing state-of-the-art methods, modified to our specific requirements – multi-currencies, in-browser verification, no external auditor – coupled with a necessity for swift implementation and delivery.
After analysing the existing literature of PoL protocols, it became clear that we had a choice between two main options:
- Standard Merkle Tree based
- Advanced cryptography-based (e.g. zk-snarks)
The first choice of a standard Merkle Tree based approach is derived from established cryptographic primitives, which can be easily implemented in almost any programming language, while the latter advanced-cryptography based protocols would require using ‘niche’ and advanced cryptographic libraries involving a much larger implementation effort.
Helping the decision further, use of well understood and simple cryptographic primitives makes the result less prone to error. For this reason, our PoL design is based on the Merkle Tree line of work initiated by the Maxwell-Todd proposal of 2013 as presented by Gregory Maxwell and Peter Todd. We studied the existing literature and working implementations to apply the latest improvements.
Who is Merkle and why does he have a Tree?
Cryptographic hash functions are the core ingredient of numerous cryptographic protocols. A hash is a function that takes an input of any size, and returns a small fixed-size output. For example: an input of ‘Satoshi’ will output the 4 digits 2341, and the input of all the text in the first book of Harry Potter will also only give the 4 digit output of 7654.
Hashes give same length outputs from different length inputs and the output cannot be traced back to the input. Because of this feature, this output, also called the ‘hash’ , is a computationally unique fingerprint of its input.
When you then take a hash of the hash a structure starts to form, reducing in size with every iteration, resembling leaves, branches and a trunk. As this sequence goes on, the data at any point in the process cannot be changed or all the next hashes would change too, leading to a structure where the input data is safe from modification.
The introduction of the Merkle Tree dates back to the invention of public-key cryptography in the late 1970s and is named after its inventor Ralph Merkle. In its simplest form, a Merkle Tree consists of a binary tree like data structure where each leaf is the hash of a block of data and every parent node is the hash of both children:
Hparent = Hash ( HA | | HB ) [ if HA and HB are respective child hash values ]
At the top, the root element ( and yes we know tree roots are at the bottom of the tree in the ground, but go with it ) contains a hash that has essentially aggregated all underlying data.
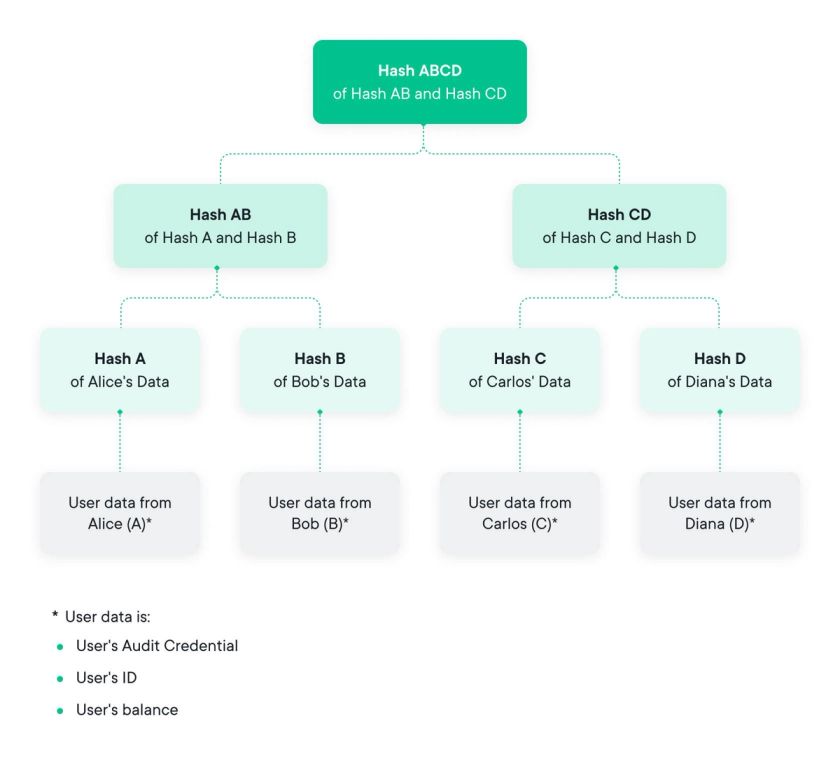
Due to the underlying properties of hash functions, it is impossible to change the data at any point of the tree without changing the root hash value; if anything is changed, the rest of the structure changes. So far, this is not very different from hashing all the data. However, what the Merkle Tree allows us to do is to aggregate a high number of data inputs – also known as blocks – in a way that is very efficient to verify the inclusion of one specific data block.
Put differently, this verification method can be used to demonstrate that a given data block was included in the tree, and that this block was on the path of the subsequent sibling nodes ( on the ‘inclusion path’ ) up to the root hash. Because of this, the size of the inclusion proof becomes logarithmic instead of linear; so for 1 million leaves, the proof contains only 20 nodes, not including the root node.
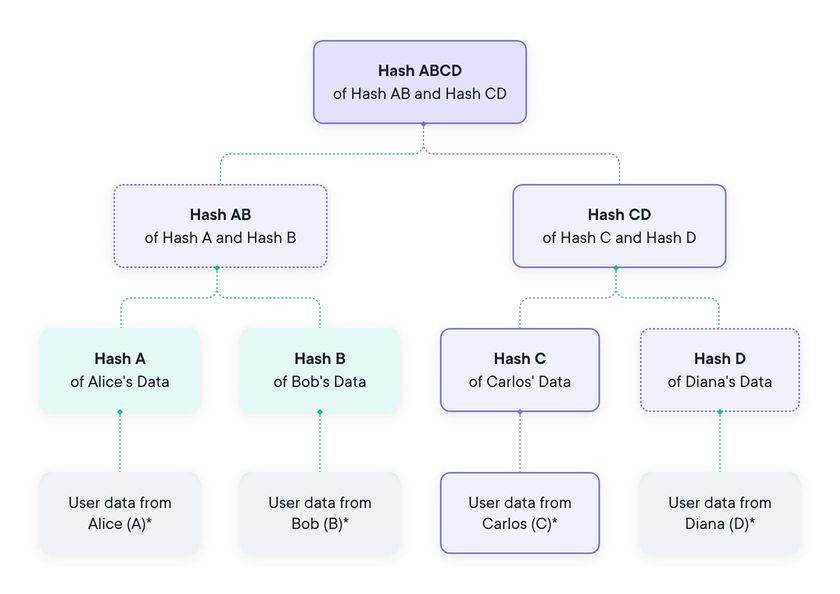
At the top of the tree, that root hash value acts as a commitment-lock because once this value is shown, the underlying data cannot be changed. On the other side of this coin, it is impossible to claim that data was included that was not there when the Merkle Tree was being built, because it is all there to see and can’t be tampered with.
The Maxwell-Todd line of PoL
As mentioned above, the first proposal for PoL based on a Merkle Tree is credited to Maxwell-Todd in 2013. Their proposal was based on using a Merkle Tree with data blocks that included a user’s balance. In addition, each node of this Merkle Tree is enhanced with a liability consisting of the sum of all liabilities of the respective child nodes. For this reason, each node is composed of a digest and a positive balance.
This way, the root node balance becomes the sum of all user liabilities. This data structure is called a ‘summation Merkle Tree’ as seen in the diagram below.
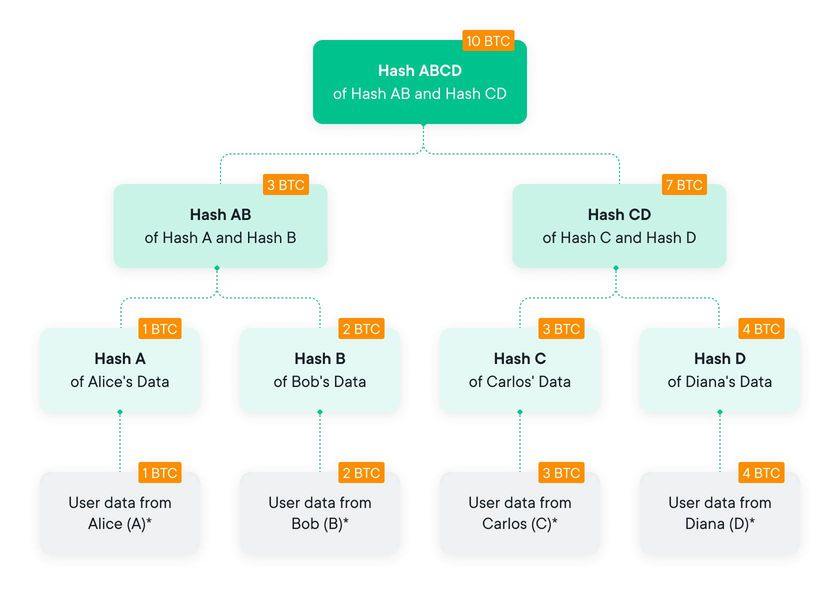
Now this is where things get interesting. The hashed value of a leaf node is obtained by hashing a user’s ID, a user’s credential, and the user’s balance. The user’s credential serves to mask the user ID; to protect the user's privacy. To improve the safety of this method, the position of the leaf node of a given user is picked at random to break the link between a user and their balance. The hashed value of any other node is computed by hashing the liabilities of the child nodes and their respective digest values.
Hparent = Hash ( BalA | | BalB | | HA | | HB )
To show a user that their liabilities are included in the Merkle Tree, the Prover provides an inclusion path. This is done in the same way as with a standard Merkle Tree, only enhanced with the liability summation.
In the validation, the user computes the parent hash, as above, and then checks the summation of the child balances. As part of this summation check, the user also checks that both BalA and BalB are positive and that BalA + BalB = Bal, where BalA, BalB are the child balances and Bal the liability of the parent. This validation step is performed at every level of the Merkle Tree, from the leaves up to the root.
We note that the above summation Merkle Tree corresponds to a slightly modified version of the original Maxwell-Todd Merkle Tree due to the application of the insights presented in an academic paper by Hu, Zhang, and Guo (2019) which fixed a security flaw. The new variant of the Merkle Tree was updated with this security flaw fix, and coined the ‘Maxwell+ Merkle Tree’ in an academic paper by Ji-Chalkias (2021); the name stuck.
Continuing this logic, in the paper of Ji-Chalkias (2021) there is mention of a method to hide original user balances by splitting each into multiple shards – an insight accredited to Chalkias, Lewi, Mohassel, and Nikolaenko in 2019 – and shuffling them at random in the tree leaves. Following the logic of nomenclature, this next variant was named the Maxwell++ Merkle Tree by Ji-Chalkias (2021).
Putting this all together, we can say that the progression of this cryptographic method for practical use on Proof of Liabilities came with Maxwell-Todd’s iteration where the Merkle Tree was able to include summation. Moving on the timeline of innovation, a security flaw was found and fixed, leading to the establishment and use of the Maxwell+ variant, and the final version where each user’s balance was split into shards in order to obfuscate the real user liabilities gave rise to Maxwell++. Each of these improvements has been important and welcomed by the community. We are glad to use this tech in our solution too.
SwissBorg’s Design Choices
Because the SwissBorg app supports multiple fiat and cryptocurrencies, users typically own a number of them. In principle, we could apply a single Merkle Tree to cover all currencies at the same time by applying the summation of balances, currency-wise. However, for many users, the breakdown of currencies in their portfolio is unique and would therefore pose a serious privacy issue.
As a mitigation, our design handles each currency separately as we build a dedicated Merkle Tree per currency. We then aggregate all Merkle Tree root data into a so-called Audit Commitment Hash which is the hash value of all currency liabilities and the respective tree root hashes.
Essentially, the whole construction can be seen as a single Merkle Tree with the difference being that the upper layer consists of as many branches as the number of currencies. Because of this feature, in order to verify the liabilities, all currency Merkle Tree roots have to be sent as part of the inclusion proof.
To further improve the privacy of user balances, we split each user balance into at least 2 positive sub-balances/shards and their positions in the Merkle Tree leaves are determined at random. For the sake of simplicity and to partially hide the number of users per currency, we always generate a number of sub-balances equal to the power of 2 so the Merkle binary tree is complete.
It’s worth noting that the splitting of balances is in line with Bitmex’s PoL solution and Maxwell++ variant with a splitting factor > 2.
Following the Maxwell++ design, user privacy is achieved by including some high-entropy masking nonces in the leaf data; based on a leaf node – the hash and balance – it is not possible to find out the corresponding user identity. This so-called ‘leaf nonce’ is derived from a per-user audit credential, which is a 128-bit random value exclusively devoted for the purposes of the PoL.
Where can I find my credential?
Your credential can be found in the security tab of the SwissBorg app. We have called it a ‘credential’ to emphasise that our users need to keep it confidential, as someone could take it and reveal a user's balances – with corresponding leaf nodes.
The credential is meant to be kept long-term and re-used over several instances of Proof of Liabilities audits. Following standard cryptographic practices, the leaf nonces are derived – with a cryptographic Key Derivation Function – in a hierarchical way:
- Audit Identifier, user audit credential → Audit Nonce
- Audit Nonce, currency → Merkle Tree Nonce
- MT Nonce, leaf index → Leaf Node nonce
- Leaf data: leaf nonce, userId, balance shard
Another important detail is that these different levels of nonces might be used to reveal information related to the user liabilities at different specificities, for example per-audit or per currency.
Of course, everyone needs a user identifier, so for this we have decided to use the SwissBorg ID, which is associated with its user at all points of the process. It can easily be found in the app, at the bottom of the Profile menu, in the form of "ID: 20XXX". This identifier never changes and is unique for each user.
The SwissBorg PoL service provides several Merkle Tree inclusion paths, one per user sub-balance shard in fact, which will be validated by a script run in the browser and will render the total balances for this user.
The validation check is performed with respect to the audit commitment hashes which will be made public via Twitter. The algorithm can be summarised as follows:
- All Merkle root nodes are checked against the ‘Audit Commitment Hash’. Additionally, the user can check that this hash corresponds to the one published on Twitter.
- For each inclusion path, the path is validated by recursively computing the parent node with the sibling node provided by the inclusion proof and verifying that the top node corresponds with one of the Merkle Tree root nodes that were validated in the previous step. As part of this process, a check is done for each sibling to make sure they have positive liabilities.
- After each successful inclusion proof validation, the corresponding user leaf balance is added to the user’s total liabilities.
- If no error has occurred, the user's total liabilities are returned to the user.
Discussion
The SwissBorg Proof of Liabilities design is based on state of the art Merkle Tree based construction, ensuring the utmost privacy of user identities and associated liabilities. In addition, we chose to emphasise easy operation and user performed self-verification, meaning that no third-party auditor needs to be involved, contrary to several other Proof of Liabilities solutions, like the one from Kraken for example.
Our approach is more in line with how Bitmex chose to do it, with the main difference being that our verification is more lightweight and accommodates a multi-currency setting.
This lightweight characteristic comes from the fact that the user doesn't need to download a full Merkle Tree, only the inclusion proofs, which represent just a small fraction of the tree. This allows for an in-browser validation that can be inspected by the user if they wish to do so.
We came to the conclusion that not publishing the full Merkle Trees is by no means a vulnerability as the audit commitment hash guarantees the integrity of underlying data – it is cryptographically impossible to change any data in the Merkle Tree afterwards.
The disclosure of the full Merkle Tree can only guarantee that the structure is well formed, in the sense that all liabilities are positive and hashes of the non-leaves nodes are correct.
Limitations
In terms of limitations, a user who is doing the validation cannot detect if a liability of another user is incorrect or has been omitted. To catch a case of manipulation by a malicious provider requires validation by the affected users irrespective of full Merkle Tree or disclosure of inclusion proofs.
Both the assurance that the total number of liabilities and the total value of the liabilities were not lowered by the provider depends on the level of involvement of users.
With this non-third party, only inclusion-proof, self-verification system, the more users that check their liabilities the better. This is because the more people are looking at the information, the greater the likelihood that if something is wrong, it will be seen, and the greater the user consensus.
This comes down to the basic concept of 'the more people are checking something, the lower the likelihood that the Prover can mess with it and not be noticed'.
In Section 5 of the previously mentioned academic paper by Ji-Chalkias, the authors present detailed computation on how many users doing inclusion proof verifications are needed to detect any misbehaviour on the part of the Prover.
There are additional limitations with our solution that pose no threat to security, and are constantly being looked at for improvements. These limitations pertain to:
- some information on individual liabilities – with absolutely no link to user IDs,
- the privacy of the number of users per currency,
- the total liabilities.
In our view the first on the list – the limitation of privacy on information on individual liabilities – has been solved with our solution through 'splitting balances' which still shows partial information, like indicating if a balance is above a certain amount, but not sensitive personal data.
To clarify, splitting balances just means that the original user balance is fragmented in sub-balances so that the sum of sub-balances = original balance. Doing this makes the original balance not appear in the Merkle Tree.
The second and third limitations pertain more to information that the provider might want to keep private and do not pose any real privacy risk to our users. The great news is that there are modern solutions being worked on based on more advanced cryptographic constructions, like zk-SNARKS, that solve these problems, giving us options in the future to implement and reduce limitations even further.
At the moment, due to their newness, these solutions are less accessible and require more development from our side. For these reasons we decided to first implement the tried and tested Merkle Tree solution as the remaining issues are not at all critical.
We are keeping tabs on all these solutions, including the much discussed Vitalik's proposal and the very promising Dapol+ solution from Ji-Chalkias as previously discussed, which first caught the attention of the cryptographic community at the Computer and Communications Security Conference, ACM CCS 2021. We will continue to innovate our solution, integrating improvements as they come; always innovating forward.
Why no third-party auditors?
While user self-verification was a strict requirement of our system, this does not exclude the possibility of the involvement of a third-party auditor in the future. One of the potential benefits of having one come on board is to increase the powers of detection and not solely rely on users' involvement to detect a fraudulent provider.
Some good examples of this positive influence include the following.
- A third-party auditor might systematically verify some samples of user liabilities against the Proof of Liabilities.
- An auditor’s involvement in the case of a dispute resolution whereby a user claims incorrect or missing liabilities in the Proof of Liabilities report.
It seems like an issue like this would be difficult to solve purely through technical means and that the involvement of a third-party auditor might help greatly. To further this point, in the security analysis of Chalkias of the Binance PoL, he touches on the fact that an auditor’s involvement could prevent the provider from tracking users who perform the verification, and omit liabilities to those who never check. All things to consider for future iterations.
How to validate
As a user, you can check and validate your liabilities by visiting the Secure with SwissBorg page on our website.
Please follow the instructions on the page and enter your personalised Audit Credential ID which can be found in the Security section of the SwissBorg app.
It is important to know that the liabilities you will see are taken at the time of the latest audit and are therefore not a ‘live’ representation of your liabilities. These audits are scheduled to happen on a regular basis, with the frequency to be announced when finally determined.
If you are confident with the term ‘GitHub repo’ and you wish to check and validate your liabilities locally on your computer, please follow the instructions in the published source code SwissBorg Proof of Liabilities Repo.
Concluding Remarks
Proving what we hold for our users has become standard practice in the crypto space, and we are proud of having independently built a solution that offers users the option to check their holdings.
The first version of the SwissBorg Proof of Liabilities Portal has been released, allowing every user to validate their corresponding liabilities with ease with no reliance on third-party auditors while achieving a high level of security and privacy.
This is an ongoing initiative and we are keeping an eye on potential developments. In particular, we may consider implementing one of the more advanced cryptographic techniques to bolster the strength of the system, like Vitalik’s proposal, when the time comes.
The topic of secure, open, user friendly and user centric proofs is a crucial topic, being worked on by many smart players and from several perspectives. That being said, it may take a while before the industry converges towards standardisation of PoL, but we see it as a positive inevitability, for everyone.
For now though, everyone counts on everyone, meaning we count on our splendid users to take a moment to validate their liabilities through the Proof of Liabilities Portal, and by so doing, to know that they are not only making sure their crypto assets are safe and accounted for, but that they are also contributing to the reinforcement of trust in SwissBorg and our amazing community.
Check your SwissBorg app account balance instantly
Disclaimer
Please note that the information on users' liabilities provided by our proof of liabilities protocol is recorded from SwissBorg's internal ledger system. SwissBorg shall not be held liable for any misstated balances resulting from any mistake or error in the ledger. It does not provide information on other liabilities or risks of the company. This article is intended for general guidance and informational purposes only and does not constitute any offer to the public of virtual assets or financial instruments, financial advice, investment advice, or any other type of advice, and should not be interpreted or understood as any form of promotion, recommendation, solicitation, offer or endorsement to (i) buy or sell any product, (ii) carry out transactions, or (iii) engage in any other legal transaction. Neither SwissBorg Solutions OÜ nor its affiliates, make any representation or warranty or guarantee as to the completeness, accuracy, timeliness or suitability of any information contained within any part of this article, nor to it being free from error.






